K Coloring Np Complete. NP-Completeness Graph Coloring Graph K-coloring Problem. A K-coloring problem for undirected graphs is an assignment of colors to the nodes of the graph such that no two adjacent vertices have the same color and at most K colors are used to complete color the graph. Remains NP-complete when restricted to the class of triangle-free graphs with maximum degree 4. Begingroup I take issue with the sentence Therefore if P1 is solved we know solution to P2. Given a graph GV E and an integer K.
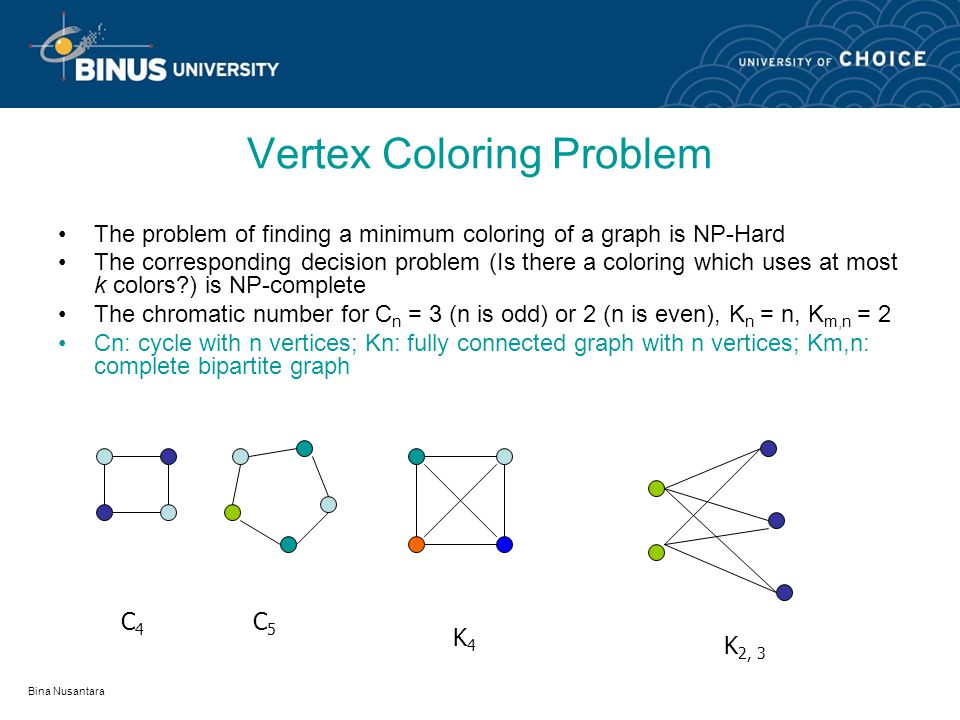
Likewise the question Is a triangle-free graph k-colorable is shown to be NP-complete for any fixed value of k. Remains NP-complete when restricted to the class of triangle-free graphs with maximum degree 4. NP-Completeness Graph Coloring Graph K-coloring Problem. A K-coloring problem for undirected graphs is an assignment of colors to the nodes of the graph such that no two adjacent vertices have the same color and at most K colors are used to complete color the graph. Given a graph GV E and an integer K.
Given a graph GV E and an integer K.
Likewise the question Is a triangle-free graph k-colorable is shown to be NP-complete for any fixed value of k. Remains NP-complete when restricted to the class of triangle-free graphs with maximum degree 4. A K-coloring problem for undirected graphs is an assignment of colors to the nodes of the graph such that no two adjacent vertices have the same color and at most K colors are used to complete color the graph. NP-Completeness Graph Coloring Graph K-coloring Problem. Likewise the question Is a triangle-free graph k-colorable is shown to be NP-complete for any fixed value of k. NP-hardness is a precise concept. Given a graph GV E and an integer K. Begingroup I take issue with the sentence Therefore if P1 is solved we know solution to P2.
